Next: 13.3 : A Doubly-Logarithmic Up: 13. Data Structures for Previous: 13.1 : A digital Contents
: Searching in Doubly-Logarithmic Time
The performance of the
structure is not that impressive.
The number of elements,
, stored in the structure is at most
,
so
. In other words, any of the comparison-based
structures described in other parts of this book are at least as efficient
as a
, and don't have the restriction of only being able to
store integers.
Next we describe the
, which is just a
with
hash tables--one for each level of the trie. These hash tables
are used to speed up the
operation to
time.
Recall that the
operation in a
is almost complete
once we reach a node,
, where the search path for
would like to
proceed to
(or
) but
has no right (respectively,
left) child. At this point, the search uses
to jump to a leaf,
, of the
and either return
or its successor in the
linked list of leaves. An
speeds up the search process by
using binary search on the levels of the trie to locate the node
.
To use binary search, we need a way to determine if the node
we are
looking for is above a particular level,
, of if
is at or below
level
. This information is given by the highest-order
bits
in the binary representation of
; these bits determine the search
path that
takes from the root to level
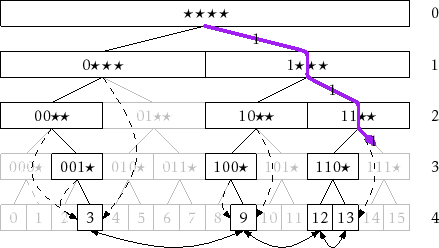
. For an example,
refer to Figure 13.6; in this figure the last node,
, on
search path for 14 (whose binary representation is 1110) is the node
labelled
at level 2 because there is no node labelled
at level 3. Thus, we can label each node at level
with an
-bit integer. Then the node
we are searching for is at
or below level
if and only if there is a node at level
whose
label matches the highest-order
bits of
.
|
In an
, we store, for each
, all
the nodes at level
in a
,
![$ \mathtt{t[i]}$](img778.png){kind=small}
, that is implemented as a
hash table (Chapter 5). Using this
allows us to check
in constant expected time if there is a node at level
whose label
matches the highest-order
bits of
. In fact, we can even find
this node using
![$ \mathtt{t[i].find(x>>(w-i))}$](img1705.png){kind=small}
.
The hash tables
![$ \ensuremath{\mathtt{t[0]}},\ldots,\ensuremath{\mathtt{t[w]}}$](img1706.png){kind=small}
allow us to use binary search
to find
. Initially, we know that
is at some level
with
. We therefore initialize
and
and repeatedly look at the hash table
, where
. If
![$ \ensuremath{\mathtt{t[i]}}$](img1711.png){kind=small}
contains a node whose label matches
's highest-order
bits then we set
(
is at or below level
), otherwise we set
(
is above level
). This process
terminates when
, in which case we determine that
is
at level
. We then complete the
operation using
and the doubly-linked list of leaves.
T find(T x) {
int l = 0, h = w+1;
unsigned ix = intValue(x);
Node *v, *u = &r;
while (h-l > 1) {
int i = (l+h)/2;
XPair<Node> p(ix >> (w-i));
if ((v = t[i].find(p).u) == NULL) {
h = i;
} else {
u = v;
l = i;
}
}
if (l == w) return u->x;
Node *pred = (((ix >> (w-l-1)) & 1) == 1) ? u->jump : u->jump->prev;
return (pred->next == &dummy) ? NULL : pred->next->x;
}
Each iteration of the
loop in the above method decreases
by roughly a factor of 2, so this loop finds
after
iterations. Each iteration performs a constant amount of work and one
operation in a
, which takes constant expected time.
The remaining work takes only constant time, so the
method in
an
takes only
expected time.
The
and
methods for an
are almost
identical to the same methods in a
. The only modifications
are for managing the hash tables
![$ \mathtt{t[0]}$](img1717.png){kind=small}
,...,
![$ \mathtt{t[w]}$](img1718.png){kind=small}
. During the
operation, when a new node is created at level
, this node
is added to
. During a
operation, when a node is
removed form level
, this node is removed from
. Since adding
and removing from a hash table take constant expected time, this does
not increase the running times of
and
by more than
a constant factor. We omit a code listing or
and
since
it is almost identical to the (long) code listing already provided
for the same methods in a
.
The following theorem summarizes the performance of an
:
implements the
interface for
-bit integers. An
supports the operations
and
in
expected time per operation and
in
expected time per operation.
that
stores
values is
.opendatastructures.org