The implicit representation of a complete binary tree as an array,
or list, seems to have been first proposed by Eytzinger [24],
as a representation for pedigree family trees. The
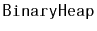 data
structure described here was first introduced by Williams [69].
data
structure described here was first introduced by Williams [69].
The randomized
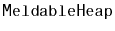 data structure described here appears
to have first been proposed by Gambin and Malinowski [31].
Other meldable heap implementations exist, including leftist heaps
[13,43, Section 5.3.2], binomial heaps [66], Fibonacci
heaps [29], pairing heaps [28], and skew heaps
[63], although none of these are as simple as the
data structure described here appears
to have first been proposed by Gambin and Malinowski [31].
Other meldable heap implementations exist, including leftist heaps
[13,43, Section 5.3.2], binomial heaps [66], Fibonacci
heaps [29], pairing heaps [28], and skew heaps
[63], although none of these are as simple as the
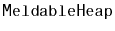 structure.
structure.
Some of the above structures also support a
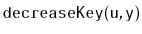 operation
in which the value stored at node
operation
in which the value stored at node
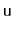 is decreased to
is decreased to
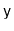 . (It is a
pre-condition that
. (It is a
pre-condition that
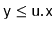 .) This operation can be implemented
in
.) This operation can be implemented
in
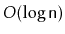 time in most of the above structures by removing node
time in most of the above structures by removing node
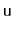 and adding
and adding
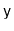 . However, some of these structures can implement
. However, some of these structures can implement
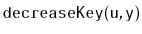 more efficiently. In particular,
more efficiently. In particular,
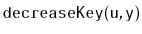 takes
takes 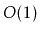 amortized time in Fibonacci heaps and
amortized time in Fibonacci heaps and
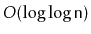 amortized time in a special version of pairing heaps [22].
This more efficient
amortized time in a special version of pairing heaps [22].
This more efficient
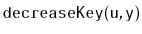 operation has applications in
speeding up several graph algorithms including Dijkstra's shortest path
algorithm [29].
operation has applications in
speeding up several graph algorithms including Dijkstra's shortest path
algorithm [29].
Exercise 10..1
Illustrate the addition of the values 7 and then 3 to the
shown at the end of Figure
10.2.
Exercise 10..2
Illustrate the removal of the next two values (6 and 8) on the
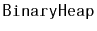
shown at the end of Figure
10.3.
Exercise 10..3
Implement the
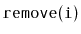
method, that removes the value stored in
![$ \mathtt{a[i]}$](img215.png)
in a
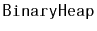
. This method should run in
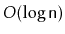
time.
Next, explain why this method is not likely to be useful.
Exercise 10..4
A
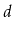
-ary tree is a generalization of a binary tree in which each
internal node has
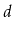
children. Using Eytzinger's method it is also
possible to represent complete
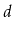
-ary trees using arrays. Work out
the equations that, given an index
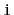
, determine the index of
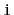
's
parent and each of
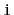
's
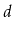
children in this representation.
Exercise 10..5
Using what you learned in Exercise
10.4, design and
implement a

, the
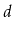
-ary generalization of a
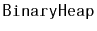
. Analyze the running times of operations on a

and test the performance of your

implementation against
that of the
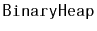
implementation given here.
Exercise 10..6
Illustrate the addition of the values 17 and then 82 in the
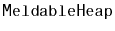
shown in Figure
10.4. Use a coin to
simulate a random bit when needed.
Exercise 10..7
Illustrate the removal of the next two values (4 and 8) in the
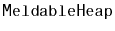
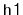
shown in Figure
10.4. Use a coin to
simulate a random bit when needed.
Exercise 10..8
Implement the
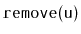
method, that removes the node
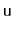
from
a
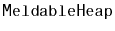
. This method should run in
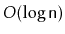
expected time.
Exercise 10..9
Show how, in a
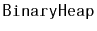
or
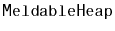
, to find the second
smallest value in constant time.
Exercise 10..10
Show how, in a
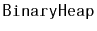
or
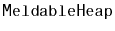
, to find the
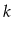
th
smallest value in
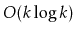
time. (Hint: Using another heap might
help.)
Exercise 10..11
Suppose you are given
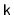
sorted lists, of total length
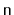
. Show how,
using a heap, to merge these into a single sorted list in
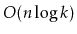
time. (Hint: Starting with the case
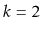
can be instructive.)
opendatastructures.org
![]() data
structure described here was first introduced by Williams [69].
data
structure described here was first introduced by Williams [69].
![]() data structure described here appears
to have first been proposed by Gambin and Malinowski [31].
Other meldable heap implementations exist, including leftist heaps
[13,43, Section 5.3.2], binomial heaps [66], Fibonacci
heaps [29], pairing heaps [28], and skew heaps
[63], although none of these are as simple as the
data structure described here appears
to have first been proposed by Gambin and Malinowski [31].
Other meldable heap implementations exist, including leftist heaps
[13,43, Section 5.3.2], binomial heaps [66], Fibonacci
heaps [29], pairing heaps [28], and skew heaps
[63], although none of these are as simple as the
![]() structure.
structure.
![]() operation
in which the value stored at node
operation
in which the value stored at node
![]() is decreased to
is decreased to
![]() . (It is a
pre-condition that
. (It is a
pre-condition that
![]() .) This operation can be implemented
in
.) This operation can be implemented
in
![]() time in most of the above structures by removing node
time in most of the above structures by removing node
![]() and adding
and adding
![]() . However, some of these structures can implement
. However, some of these structures can implement
![]() more efficiently. In particular,
more efficiently. In particular,
![]() takes
takes ![]() amortized time in Fibonacci heaps and
amortized time in Fibonacci heaps and
![]() amortized time in a special version of pairing heaps [22].
This more efficient
amortized time in a special version of pairing heaps [22].
This more efficient
![]() operation has applications in
speeding up several graph algorithms including Dijkstra's shortest path
algorithm [29].
operation has applications in
speeding up several graph algorithms including Dijkstra's shortest path
algorithm [29].