The term scapegoat tree is due to Galperin and Rivest [33],
who define and analyze these trees. However, the same structure
was discovered earlier by Andersson [5,7], who called them
general balanced trees
since they can have any shape as long as
their height is small.
Experimenting with the ScapegoatTree implementation will reveal that
it is often considerably slower than the other SSet implementations
in this book. This may be somewhat surprising, since height bound of
is better than the expected length of a search path in a Skiplist and
not too far from that of a Treap. The implementation could be optimized
by storing the sizes of subtrees explicitly at each node or by reusing
already computed subtree sizes (Exercises 8.5
and 8.6). Even with these optimizations,
there will always be sequences of
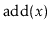 and
and
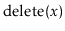 operation for
which a ScapegoatTree takes longer than other SSet implementations.
operation for
which a ScapegoatTree takes longer than other SSet implementations.
This gap in performance is due to the fact that, unlike the other SSet
implementations discussed in this book, a ScapegoatTree can spend a lot
of time restructuring itself. Exercise 8.3 asks you to prove
that there are sequences of
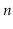 operations in which a ScapegoatTree
will spend on the order of
operations in which a ScapegoatTree
will spend on the order of
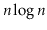 time in calls to
time in calls to
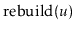 .
This is in contrast to other SSet implementations discussed in this
book, which only make
.
This is in contrast to other SSet implementations discussed in this
book, which only make
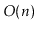 structural changes during a sequence
of
structural changes during a sequence
of
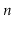 operations. This is, unfortunately, a necessary consequence of
the fact that a ScapegoatTree does all its restructuring by calls to
operations. This is, unfortunately, a necessary consequence of
the fact that a ScapegoatTree does all its restructuring by calls to
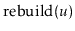 [20].
[20].
Despite their lack of performance, there are applications in which a
ScapegoatTree could be the right choice. This would occur any time
there is additional data associated with nodes that cannot be updated
in constant time when a rotation is performed, but that can be updated
during a
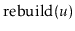 operation. In such cases, the ScapegoatTree
and related structures based on partial rebuilding may work. An example of such an application is outlined in Exercise 8.11.
operation. In such cases, the ScapegoatTree
and related structures based on partial rebuilding may work. An example of such an application is outlined in Exercise 8.11.
Exercise 8..1
Illustrate the addition of the values 1.5 and then 1.6 on the
ScapegoatTree in Figure
8.1.
Exercise 8..2
Illustrate what happens when the sequence
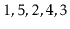
is added to an
empty ScapegoatTree, and show where the credits described in the
proof of Lemma
8.3 go, and how they are used during
this sequence of additions.
Exercise 8..3
Show that, if we start with an empty ScapegoatTree and call
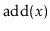
for
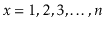
, then the total time spent during calls to
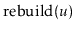
is at least
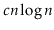
for some constant
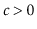
.
Exercise 8..5
Modify the
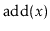
method of the ScapegoatTree so that it does not
waste any time recomputing the sizes of subtrees that have already
been computed. This is possible because, by the time the method
wants to compute
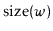
, it has already computed one of
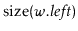
or
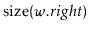
. Compare the performance of your modified
implementation with the implementation given here.
Exercise 8..6
Implement a second version of the ScapegoatTree data structure that
explicitly stores and maintains the sizes of the subtree rooted at
each node. Compare the performance of the resulting implementation
with that of the original ScapegoatTree implementation as well as
the implementation from Exercise
8.5.
Exercise 8..7
Reimplement the
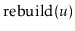
method discussed at the beginning of this
chapter so that it does not require the use of an array to store the
nodes of the subtree being rebuilt. Instead, it should use recursion
to first connect the nodes into a linked list and then convert this
linked list into a perfectly balanced binary tree. (There are
very elegant recursive implementations of both steps.)
Exercise 8..8
Analyze and implement a WeightBalancedTree. This is a tree in
which each node
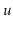
, except the root, maintains the
balance
invariant that
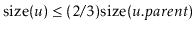
. The
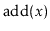
and
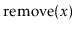
operations are identical to the standard BinarySearchTree
operations, except that any time the balance invariant is violated at
a node
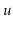
, the subtree rooted at
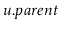
is rebuilt.
Your analysis should show that operations on a WeightBalancedTree
run in
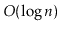
amortized time.
Exercise 8..9
Analyze and implement a CountdownTree. In a CountdownTree each
node
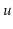
keeps a
timer
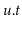
. The
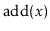
and
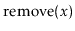
operations are exactly the same as in a standard BinarySearchTree
except that, whenever one of these operations affects
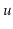
's subtree,
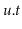
is decremented. When
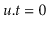
the entire subtree rooted at
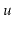
is rebuilt into a perfectly balanced binary search tree. When a node
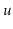
is involved in a rebuilding operation (either because
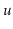
is rebuilt
or one of
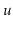
's ancestors is rebuilt)
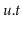
is reset to
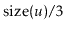
.
Your analysis should show that operations on a CountdownTree run
in
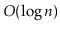 amortized time. (Hint: First show that each node
amortized time. (Hint: First show that each node
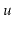 satisfies some version of a balance invariant.)
satisfies some version of a balance invariant.)
Exercise 8..10
Analyze and implement a DynamiteTree. In a DynamiteTree each
node
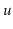
keeps tracks of the size of the subtree rooted at
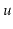
in a
variable
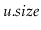
. The
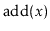
and
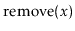
operations are exactly
the same as in a standard BinarySearchTree except that, whenever one
of these operations affects a node
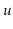
's subtree,
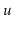 explodes
explodes
with probability
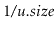
. When
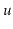
explodes, its entire subtree
is rebuilt into a perfectly balanced binary search tree.
Your analysis should show that operations on a DynamiteTree run
in
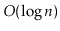 expected time.
expected time.
opendatastructures.org
![]() operations in which a ScapegoatTree
will spend on the order of
operations in which a ScapegoatTree
will spend on the order of
![]() time in calls to
time in calls to
![]() .
This is in contrast to other SSet implementations discussed in this
book, which only make
.
This is in contrast to other SSet implementations discussed in this
book, which only make
![]() structural changes during a sequence
of
structural changes during a sequence
of
![]() operations. This is, unfortunately, a necessary consequence of
the fact that a ScapegoatTree does all its restructuring by calls to
operations. This is, unfortunately, a necessary consequence of
the fact that a ScapegoatTree does all its restructuring by calls to
![]() [20].
[20].
![]() operation. In such cases, the ScapegoatTree
and related structures based on partial rebuilding may work. An example of such an application is outlined in Exercise 8.11.
operation. In such cases, the ScapegoatTree
and related structures based on partial rebuilding may work. An example of such an application is outlined in Exercise 8.11.
![]() amortized time. (Hint: First show that each node
amortized time. (Hint: First show that each node
![]() satisfies some version of a balance invariant.)
satisfies some version of a balance invariant.)![]() expected time.
expected time. ![]() in constant time,
each element
in constant time,
each element
![]() is labelled with an integer that encodes the path from
the root to
is labelled with an integer that encodes the path from
the root to
![]() . In this way,
. In this way,
![]() can be implemented
by comparing the labels of
can be implemented
by comparing the labels of
![]() and
and
![]() .
.