Red-black trees were first introduced by Guibas and Sedgewick [38].
Despite their high implementation complexity they are found in some of
the most commonly used libraries and applications. Most algorithms and
data structures textbooks discuss some variant of red-black trees.
Andersson [6] describes a left-leaning version of balanced trees
that is similar to red-black trees but has the additional constraint
that any node has at most one red child. This implies that these trees
simulate 2-3 trees rather than 2-4 trees. They are significantly simpler,
though, than the RedBlackTree structure presented in this chapter.
Sedgewick [66] describes two versions of left-leaning red-black
trees. These use recursion along with a simulation of top-down splitting
and merging in 2-4 trees. The combination of these two techniques makes
for particularly short and elegant code.
A related, and older, data structure is the AVL tree [3].
AVL trees are height-balanced:
At each node 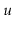 , the height
of the subtree rooted at
, the height
of the subtree rooted at
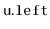 and the subtree rooted at
and the subtree rooted at
 differ by at most one. It follows immediately that, if
differ by at most one. It follows immediately that, if 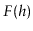 is the
minimum number of leaves in a tree of height
is the
minimum number of leaves in a tree of height 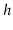 , then
, then 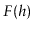 obeys the
Fibonacci recurrence
obeys the
Fibonacci recurrence
with base cases 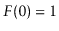 and
and 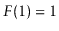 . This means
. This means 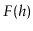 is approximately
is approximately
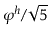 , where
, where
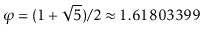 is the
golden ratio. (More precisely,
is the
golden ratio. (More precisely,
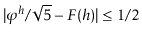 .)
Arguing as in the proof of Lemma 9.1, this implies
.)
Arguing as in the proof of Lemma 9.1, this implies
so AVL trees have smaller height than red-black trees. The height
balancing can be maintained during
 and
and
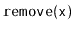 operations
by walking back up the path to the root and performing a rebalancing
operation at each node
operations
by walking back up the path to the root and performing a rebalancing
operation at each node
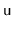 where the height of
where the height of
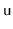 's left and right
subtrees differ by two. See Figure 9.10.
's left and right
subtrees differ by two. See Figure 9.10.
Figure 9.10:
Rebalancing in an AVL tree. At most two rotations are required
to convert a node whose subtrees have a height of 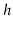 and
and 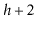 into a node
whose subtrees each have a height of at most
into a node
whose subtrees each have a height of at most 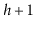 .
.
|
|
Andersson's variant of red-black trees, Sedgewick's variant of red-black
trees, and AVL trees are all simpler to implement than the RedBlackTree
structure defined here. Unfortunately, none of them can guarantee that
the amortized time spent rebalancing is 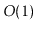 per update. In particular,
there is no analogue of Theorem 9.2 for those structures.
per update. In particular,
there is no analogue of Theorem 9.2 for those structures.
Figure 9.11:
A red-black tree on which to practice.
|
![\includegraphics[scale=0.90909]{figs/redblack-example}](img3792.png) |
Exercise 9..1
Illustrate the 2-4 tree that corresponds to the
RedBlackTree in
Figure
9.11.
Exercise 9..2
Illustrate the addition of 13, then 3.5, then 3.3 on the
RedBlackTree
in Figure
9.11.
Exercise 9..3
Illustrate the removal of 11, then 9, then 5 on the
RedBlackTree in
Figure
9.11.
Exercise 9..4
Show that, for arbitrarily large values of
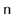
, there are red-black
trees with
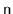
nodes that have height
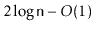
.
Exercise 9..5
Consider the operations
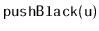
and
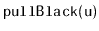
. What do
these operations do to the underlying 2-4 tree that is being simulated
by the red-black tree?
Exercise 9..6
Show that, for arbitrarily large values of
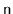
, there exist sequences
of
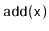
and
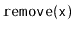
operations that lead to red-black trees
with
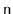
nodes that have height
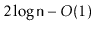
.
Exercise 9..7
Why does the method
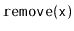
in the
RedBlackTree implementation
perform the assignment
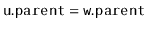
? Shouldn't this already
be done by the call to
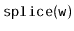
?
Exercise 9..9
Suppose you are given a binary search tree with
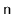
nodes and a
height of at most
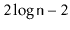
. Is it always possible to colour the
nodes red and black so that the tree satisfies the black-height and
no-red-edge properties? If so, can it also be made to satisfy the
left-leaning property?
Exercise 9..10
Suppose you have two red-black trees
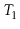
and
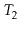
that have the
same black height,
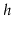
, and such that the largest key in
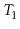
is smaller
than the smallest key in
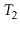
. Show how to merge
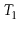
and
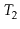
into a single red-black tree in
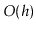
time.
Exercise 9..11
Extend your solution to Exercise
9.10 to the case where the
two trees
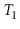
and
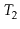
have different black heights,
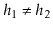
.
The running-time should be
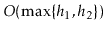
.
Exercise 9..12
Prove that, during an
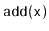
operation, an AVL tree must perform
at most one rebalancing operation (that involves at most two rotations;
see Figure
9.10). Give an example of an AVL tree and a
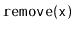
operation on that tree that requires on the order of
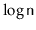
rebalancing operations.
Exercise 9..13
Implement an
AVLTree class that implements AVL trees as described
above. Compare its performance to that of the
RedBlackTree
implementation. Which implementation has a faster
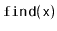
operation?
Exercise 9..14
Design and implement a series of experiments that compare the relative
performance of
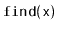
,
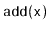
, and
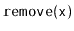
for the
SSet implemeentations
SkiplistSSet,
ScapegoatTree,
Treap, and
RedBlackTree. Be sure to include
multiple test scenarios, including cases where the data is random,
already sorted, is removed in random order, is removed in sorted order,
and so on.
opendatastructures.org
![]() , the height
of the subtree rooted at
, the height
of the subtree rooted at
![]() and the subtree rooted at
and the subtree rooted at
![]() differ by at most one. It follows immediately that, if
differ by at most one. It follows immediately that, if ![]() is the
minimum number of leaves in a tree of height
is the
minimum number of leaves in a tree of height ![]() , then
, then ![]() obeys the
Fibonacci recurrence
obeys the
Fibonacci recurrence
![\includegraphics[scale=0.90909]{figs/avl-rebalance}](img3784.png)
![]() per update. In particular,
there is no analogue of Theorem 9.2 for those structures.
per update. In particular,
there is no analogue of Theorem 9.2 for those structures.