Random binary search trees have been studied extensively. Devroye
[19] gives a proof of Lemma 7.1 and related results. There are
much stronger results in the literature as well, the most impressive
of which is due to Reed [64], who shows that the expected height
of a random binary search tree is
where
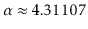 is the unique solution on the
interval
is the unique solution on the
interval
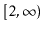 of the equation
of the equation
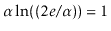 and
and
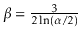 . Furthermore, the variance of the
height is constant.
. Furthermore, the variance of the
height is constant.
The name Treap was coined by Seidel and Aragon [67] who discussed
Treaps and some of their variants. However, their basic structure was
studied much earlier by Vuillemin [76] who called them Cartesian
trees.
One possible space-optimization of the Treap data structure
is the elimination of the explicit storage of the priority
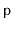 in each node. Instead, the priority of a node,
in each node. Instead, the priority of a node,
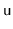 , is computed by
hashing
, is computed by
hashing
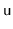 's address in memory (in 32-bit Java, this is equivalent
to hashing
's address in memory (in 32-bit Java, this is equivalent
to hashing
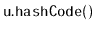 ). Although a number of hash functions will
probably work well for this in practice, for the important parts of the
proof of Lemma 7.1 to remain valid, the hash function should be randomized
and have the min-wise independent property:
For any distinct
values
). Although a number of hash functions will
probably work well for this in practice, for the important parts of the
proof of Lemma 7.1 to remain valid, the hash function should be randomized
and have the min-wise independent property:
For any distinct
values
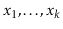 , each of the hash values
, each of the hash values
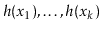 should be distinct with high probability and, for each
should be distinct with high probability and, for each
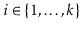 ,
,
for some constant 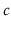 .
One such class of hash functions that is easy to implement and fairly
fast is tabulation hashing (Section 5.2.3).
.
One such class of hash functions that is easy to implement and fairly
fast is tabulation hashing (Section 5.2.3).
Another Treap variant that doesn't store priorities at each node is
the randomized binary search tree
of Martínez and Roura [51].
In this variant, every node,
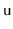 , stores the size,
, stores the size,
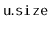 , of the
subtree rooted at
, of the
subtree rooted at
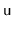 . Both the
. Both the
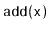 and
and
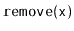 algorithms are
randomized. The algorithm for adding
algorithms are
randomized. The algorithm for adding
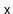 to the subtree rooted at
to the subtree rooted at
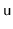 does the following:
does the following:
- With probability
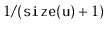 , the value
, the value
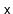 is added
the usual way, as a leaf, and rotations are then done to bring
is added
the usual way, as a leaf, and rotations are then done to bring
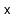 up to the root of this subtree.
up to the root of this subtree.
- Otherwise (with probability
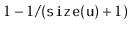 ), the value
), the value
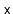 is recursively added into one of the two subtrees rooted at
is recursively added into one of the two subtrees rooted at
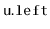 or
or
 , as appropriate.
, as appropriate.
The first case corresponds to an
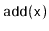 operation in a Treap where
operation in a Treap where
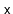 's node receives a random priority that is smaller than any of the
's node receives a random priority that is smaller than any of the
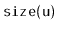 priorities in
priorities in
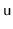 's subtree, and this case occurs with exactly
the same probability.
's subtree, and this case occurs with exactly
the same probability.
Removing a value
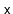 from a randomized binary search tree is similar
to the process of removing from a Treap. We find the node,
from a randomized binary search tree is similar
to the process of removing from a Treap. We find the node,
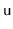 ,
that contains
,
that contains
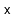 and then perform rotations that repeatedly increase
the depth of
and then perform rotations that repeatedly increase
the depth of
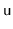 until it becomes a leaf, at which point we can splice
it from the tree. The choice of whether to perform a left or right
rotation at each step is randomized.
until it becomes a leaf, at which point we can splice
it from the tree. The choice of whether to perform a left or right
rotation at each step is randomized.
- With probability
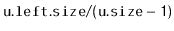 , we perform a right
rotation at
, we perform a right
rotation at
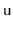 , making
, making
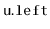 the root of the subtree that was
formerly rooted at
the root of the subtree that was
formerly rooted at
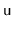 .
.
- With probability
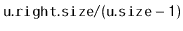 , we perform a left
rotation at
, we perform a left
rotation at
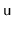 , making
, making
 the root of the subtree that was
formerly rooted at
the root of the subtree that was
formerly rooted at
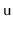 .
.
Again, we can easily verify that these are exactly the same probabilities
that the removal algorithm in a Treap will perform a left or right
rotation of
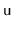 .
.
Randomized binary search trees have the disadvantage, compared to treaps,
that when adding and removing elements they make many random choices, and
they must maintain the sizes of subtrees. One advantage of randomized
binary search trees over treaps is that subtree sizes can serve another
useful purpose, namely to provide access by rank in
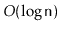 expected
time (see Exercise 7.10). In comparison, the random priorities
stored in treap nodes have no use other than keeping the treap balanced.
expected
time (see Exercise 7.10). In comparison, the random priorities
stored in treap nodes have no use other than keeping the treap balanced.
Exercise 7..1
Illustrate the addition of 4.5 (with priority 7) and then 7.5 (with
priority 20) on the
Treap in Figure
7.5.
Exercise 7..2
Illustrate the removal of 5 and then 7 on the
Treap in Figure
7.5.
Exercise 7..3
Prove the assertion that there are
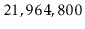
sequences that generate
the tree on the right hand side of Figure
7.1. (Hint: Give a
recursive formula for the number of sequences that generate a complete
binary tree of height
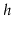
and evaluate this formula for
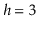
.)
Exercise 7..4
Design and implement the
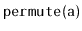
method that takes as input an
array,
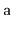
, that contains
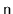
distinct values and randomly permutes
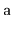
.
The method should run in
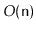
time and you should prove that each
of the
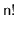
possible permutations of
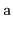
is equally probable.
Exercise 7..5
Use both parts of Lemma
7.2 to prove that the expected number
of rotations performed by an
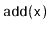
operation (and hence also a
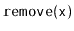
operation) is
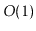
.
Exercise 7..6
Modify the
Treap implementation given here so that it does not
explicitly store priorities. Instead, it should simulate them by
hashing the
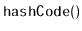
of each node.
Exercise 7..7
Suppose that a binary search tree stores, at each node,
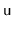
, the height,
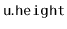
, of the subtree rooted at
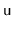
, and the size,
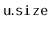
of
the subtree rooted at
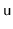
.
- Show how, if we perform a left or right
rotation at
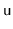 , then these two quantities can be updated, in
constant time, for all nodes affected by the rotation.
, then these two quantities can be updated, in
constant time, for all nodes affected by the rotation.
- Explain why the same result is not possible if we try to
also store the depth,
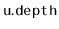 , of each node
, of each node
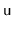 .
.
Exercise 7..8
Design and implement an algorithm that constructs a
Treap from a
sorted array,
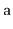
, of
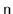
elements. This method should run in
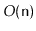
worst-case time and should construct a
Treap that is indistinguishable
from one in which the elements of
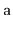
were added one at a time using
the
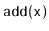
method.
Exercise 7..10
Design and implement a version of a
Treap that includes a
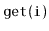
operation that returns the key with rank
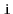
in the
Treap. (Hint:
Have each node,
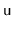
, keep track of the size of the subtree rooted
at
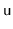
.)
Exercise 7..11
Implement a
TreapList, an implementation of the
List interface
as a treap. Each node in the treap should store a list item, and an
in-order traversal of the treap finds the items in the same order that
they occur in the list. All the
List operations
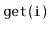
,
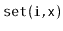
,
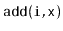
and
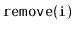
should run in
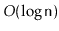
expected time.
Exercise 7..12
Design and implement a version of a
Treap that supports the
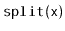
operation. This operation removes all values from the
Treap that
are greater than
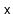
and returns a second
Treap that contains all
the removed values.
Example: the code
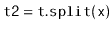 removes from
removes from
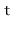 all values
greater than
all values
greater than
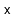 and returns a new Treap
and returns a new Treap
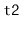 containing all
these values. The
containing all
these values. The
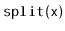 operation should run in
operation should run in
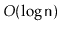 expected time.
expected time.
Warning: For this modification to work properly and still allow the
 method to run in constant time, it is necessary to implement
the modifications in Exercise 7.10.
method to run in constant time, it is necessary to implement
the modifications in Exercise 7.10.
Exercise 7..13
Design and implement a version of a
Treap that supports the
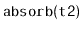
operation, which can be thought of as the inverse of
the
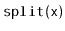
operation. This operation removes all values from the
Treap
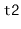
and adds them to the receiver. This operation presupposes
that the smallest value in
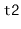
is greater than the largest value in
the receiver. The
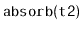
operation should run in
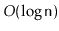
expected time.
Exercise 7..14
Implement Martinez's randomized binary search trees, as discussed in
this section. Compare the performance of your implementation with
that of the Treap implementation.
opendatastructures.org
![]() in each node. Instead, the priority of a node,
in each node. Instead, the priority of a node,
![]() , is computed by
hashing
, is computed by
hashing
![]() 's address in memory (in 32-bit Java, this is equivalent
to hashing
's address in memory (in 32-bit Java, this is equivalent
to hashing
![]() ). Although a number of hash functions will
probably work well for this in practice, for the important parts of the
proof of Lemma 7.1 to remain valid, the hash function should be randomized
and have the min-wise independent property:
For any distinct
values
). Although a number of hash functions will
probably work well for this in practice, for the important parts of the
proof of Lemma 7.1 to remain valid, the hash function should be randomized
and have the min-wise independent property:
For any distinct
values
![]() , each of the hash values
, each of the hash values
![]() should be distinct with high probability and, for each
should be distinct with high probability and, for each
![]() ,
,
![]() , stores the size,
, stores the size,
![]() , of the
subtree rooted at
, of the
subtree rooted at
![]() . Both the
. Both the
![]() and
and
![]() algorithms are
randomized. The algorithm for adding
algorithms are
randomized. The algorithm for adding
![]() to the subtree rooted at
to the subtree rooted at
![]() does the following:
does the following:
![]() from a randomized binary search tree is similar
to the process of removing from a Treap. We find the node,
from a randomized binary search tree is similar
to the process of removing from a Treap. We find the node,
![]() ,
that contains
,
that contains
![]() and then perform rotations that repeatedly increase
the depth of
and then perform rotations that repeatedly increase
the depth of
![]() until it becomes a leaf, at which point we can splice
it from the tree. The choice of whether to perform a left or right
rotation at each step is randomized.
until it becomes a leaf, at which point we can splice
it from the tree. The choice of whether to perform a left or right
rotation at each step is randomized.
![]() expected
time (see Exercise 7.10). In comparison, the random priorities
stored in treap nodes have no use other than keeping the treap balanced.
expected
time (see Exercise 7.10). In comparison, the random priorities
stored in treap nodes have no use other than keeping the treap balanced.
![]() removes from
removes from
![]() all values
greater than
all values
greater than
![]() and returns a new Treap
and returns a new Treap
![]() containing all
these values. The
containing all
these values. The
![]() operation should run in
operation should run in
![]() expected time.
expected time.
![]() method to run in constant time, it is necessary to implement
the modifications in Exercise 7.10.
method to run in constant time, it is necessary to implement
the modifications in Exercise 7.10.