Skiplists were introduced by Pugh [60] who also presented
a number of applications and extensions of skiplists [59]. Since then they
have been studied extensively. Several researchers have done very
precise analyses of the expected length and variance of the length of the
search path for the
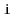 th element in a skiplist [45,44,56].
Deterministic versions [53], biased versions [8,26],
and self-adjusting versions [12] of skiplists have all been
developed. Skiplist implementations have been written for various
languages and frameworks and have been used in open-source database
systems [69,61]. A variant of skiplists is used in the HP-UX
operating system kernel's process management structures [42].
th element in a skiplist [45,44,56].
Deterministic versions [53], biased versions [8,26],
and self-adjusting versions [12] of skiplists have all been
developed. Skiplist implementations have been written for various
languages and frameworks and have been used in open-source database
systems [69,61]. A variant of skiplists is used in the HP-UX
operating system kernel's process management structures [42].
Exercise 4..1
Illustrate the search paths for 2.5 and 5.5 on the skiplist in
Figure
4.1.
Exercise 4..2
Illustrate the addition of the values 0.5 (with a height of 1) and
then 3.5 (with a height of 2) to the skiplist in Figure
4.1.
Exercise 4..3
Illustrate the removal of the values 1 and then 3 from the skiplist
in Figure
4.1.
Exercise 4..4
Illustrate the execution of
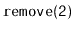
on the

in Figure
4.5.
Exercise 4..5
Illustrate the execution of
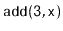
on the

in Figure
4.5. Assume that

selects a height
of 4 for the newly created node.
Exercise 4..6
Show that, during an
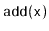
or a
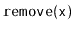
operation, the expected
number of pointers in a
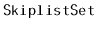
that get changed is constant.
Exercise 4..7
Suppose that, instead of promoting an element from
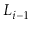
into
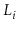
based on a coin toss, we promote it with some probability
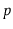
,
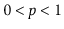
.
- Show that, with this modification, the expected length of a
search path is at most
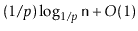 .
.
- What is the value of
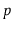 that minimizes the preceding expression?
that minimizes the preceding expression?
- What is the expected height of the skiplist?
- What is the expected number of nodes in the skiplist?
Exercise 4..8
The
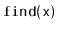
method in a
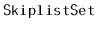
sometimes performs
redundant comparisons; these occur when
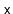
is compared to the
same value more than once. They can occur when, for some node,
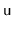
,
![$ \ensuremath{\mathtt{u.next[r]}} = \ensuremath{\mathtt{u.next[r-1]}}$](img2339.png)
. Show how these redundant comparisons
happen and modify
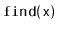
so that they are avoided. Analyze the
expected number of comparisons done by your modified
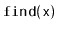
method.
Exercise 4..9
Design and implement a version of a skiplist that implements the
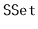
interface, but also allows fast access to elements by rank.
That is, it also supports the function
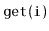
, which returns the
element whose rank is
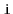
in
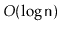
expected time. (The rank
of an element
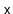
in an
is the number of elements in the
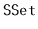
that are less than
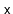
.)
Exercise 4..11
Write a method,
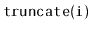
, that truncates a

at position
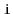
. After the execution of this method, the size
of the list is
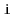
and it contains only the elements at indices
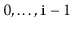
. The return value is another

that
contains the elements at indices
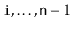
. This method
should run in
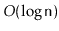
time.
Exercise 4..12
Write a

method,
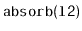
, that takes as an
argument a

,
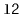
, empties it and appends its contents,
in order, to the receiver. For example, if
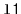
contains
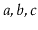
and
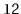
contains
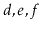
, then after calling

,
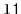
will contain
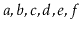
and
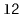
will be empty. This method should
run in
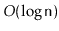
time.
Exercise 4..13
Using the ideas from the space-efficient list,

, design
and implement a space-efficient
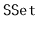
,
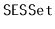
. To do this, store the
data, in order, in an

, and store the blocks of this

in an
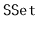
. If the original
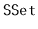
implementation uses
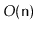
space to store
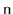
elements, then the
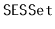
will use enough space
for
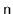
elements plus
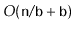
wasted space.
Exercise 4..14
Using an
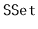
as your underlying structure, design and implement an
application that reads a (large) text file and allows you to search,
interactively, for any substring contained in the text. As the user
types their query, a matching part of the text (if any) should appear
as a result.
Hint 1: Every substring is a prefix of some suffix, so it
suffices to store all suffixes of the text file.
Hint 2: Any suffix can be represented compactly as a single
integer indicating where the suffix begins in the text.
Test your application on some large texts, such as some of
the books available at Project Gutenberg [1]. If done
correctly, your applications will be very responsive; there should be
no noticeable lag between typing keystrokes and seeing the results.
Exercise 4..15
(This exercise should be done after reading about binary search trees,
in Section
6.2.) Compare skiplists with binary search
trees in the following ways:
- Explain how removing some edges of a skiplist leads to
a structure that looks like a binary tree and is similar to a
binary search tree.
- Skiplists and binary search trees each use about the same
number of pointers (2 per node). Skiplists make better use of
those pointers, though. Explain why.
opendatastructures.org
![]() th element in a skiplist [45,44,56].
Deterministic versions [53], biased versions [8,26],
and self-adjusting versions [12] of skiplists have all been
developed. Skiplist implementations have been written for various
languages and frameworks and have been used in open-source database
systems [69,61]. A variant of skiplists is used in the HP-UX
operating system kernel's process management structures [42].
th element in a skiplist [45,44,56].
Deterministic versions [53], biased versions [8,26],
and self-adjusting versions [12] of skiplists have all been
developed. Skiplist implementations have been written for various
languages and frameworks and have been used in open-source database
systems [69,61]. A variant of skiplists is used in the HP-UX
operating system kernel's process management structures [42].
![[*]](crossref.png) is a finger; the shaded nodes in
Figure 4.3 show the contents of the finger.) One can
think of a finger as pointing out the path to a node in the lowest
list,
is a finger; the shaded nodes in
Figure 4.3 show the contents of the finger.) One can
think of a finger as pointing out the path to a node in the lowest
list, ![]() operation using a
finger, by walking up the list using the finger until reaching a node
operation using a
finger, by walking up the list using the finger until reaching a node
![]() such that
such that
![]() and
and
![]() or
or
![]() and then performing a normal search for
and then performing a normal search for
![]() starting from
starting from
![]() .
It is possible to prove that the expected number of steps required
for a finger search is
.
It is possible to prove that the expected number of steps required
for a finger search is
![]() , where
, where ![]() is the number values
in
is the number values
in ![]() between
between
![]() and the value pointed to by the finger.
and the value pointed to by the finger.
![]() called
called
![]() that
implements
that
implements
![]() operations using an internal finger. This subclass
stores a finger, which is then used so that every
operations using an internal finger. This subclass
stores a finger, which is then used so that every
![]() operation
is implemented as a finger search. During each
operation
is implemented as a finger search. During each
![]() operation
the finger is updated so that each
operation
the finger is updated so that each
![]() operation uses, as a
starting point, a finger that points to the result of the previous
operation uses, as a
starting point, a finger that points to the result of the previous
![]() operation.
operation.