Both singly-linked and doubly-linked lists are established techniques,
having been used in programs for over 40 years. They are discussed,
for example, by Knuth [46, Sections 2.2.3-2.2.5]. Even the
 data structure seems to be a well-known data structures exercise.
The
data structure seems to be a well-known data structures exercise.
The
 is sometimes referred to as an unrolled linked list
[67].
is sometimes referred to as an unrolled linked list
[67].
Another way to save space in a doubly-linked list is to use
so-called XOR-lists.
In an XOR-list, each node,
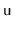 , contains only one
pointer, called
, contains only one
pointer, called
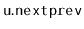 , that holds the bitwise exclusive-or of
, that holds the bitwise exclusive-or of
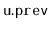 and
and
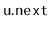 . The list itself needs to store two pointers, one to the
. The list itself needs to store two pointers, one to the
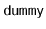 node and one to
node and one to
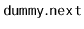 (the first node, or
(the first node, or
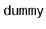 if the list is
empty). This technique uses the fact that, if we have pointers to
if the list is
empty). This technique uses the fact that, if we have pointers to
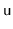 and
and
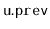 , then we can extract
, then we can extract
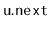 using the formula
using the formula
(Here ^ computes the bitwise exclusive-or of its two arguments.)
This technique complicates the code a little and is not possible in
some languages, like Java and Python, that have garbage collection but gives a
doubly-linked list implementation that requires only one pointer per node.
See Sinha's magazine article [68] for a detailed discussion of
XOR-lists.
Exercise 3..1
Why is it not possible to use a dummy node in an
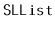
to avoid
all the special cases that occur in the operations
,
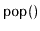
,
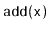
, and

?
Exercise 3..2
Design and implement an
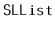
method,
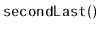
, that returns
the second-last element of an
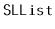
. Do this without using the
member variable,
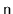
, that keeps track of the size of the list.
Exercise 3..3
Implement the

operations
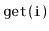
,
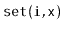
,
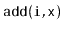
and
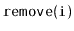
on an
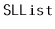
. Each of these operations
should run in
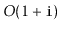
time.
Exercise 3..4
Design and implement an
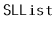
method,
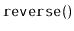
that reverses the
order of elements in an
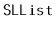
. This method should run in
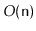
time, should not use recursion, should not use any secondary data
structures, and should not create any new nodes.
Exercise 3..5
Design and implement
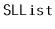
and
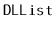
methods called
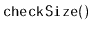
.
These methods walk through the list and count the number of nodes to
see if this matches the value,
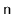
, stored in the list. These methods
return nothing, but throw an exception if the size they compute does
not match the value of
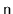
.
Exercise 3..6
Try to recreate the code for the
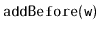
operation that creates a
node,
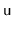
, and adds it in a
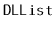
just before the node
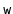
. Do not
refer to this chapter. Even if your code does not exactly match the
code given in this book it may still be correct. Test it and see if
it works.
The next few exercises involve performing manipulations on
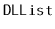 s.
You should complete them without allocating any new nodes or temporary
arrays. They can all be done only by changing the
s.
You should complete them without allocating any new nodes or temporary
arrays. They can all be done only by changing the
 and
and
 values of existing nodes.
values of existing nodes.
Exercise 3..7
Write a
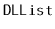
method

that returns

if the
list is a
palindrome,
i.e., the element at position
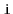
is equal to
the element at position
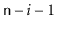
for all
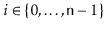
.
Your code should run in
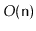
time.
Exercise 3..8
Implement a method

that ``rotates'' a
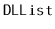
so that list
item
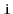
becomes list item
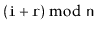
. This method should
run in
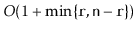
time and should not modify any nodes in
the list.
Exercise 3..9
Write a method,
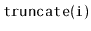
, that truncates a
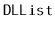
at position
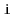
. After executing this method, the size of the list will be
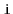
and
it should contain only the elements at indices
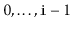
. The
return value is another
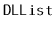
that contains the elements at indices
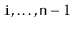
. This method should run in
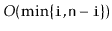
time.
Exercise 3..10
Write a
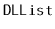
method,
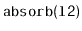
, that takes as an argument
a
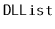
,
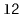
, empties it and appends its contents, in order,
to the receiver. For example, if
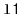
contains
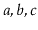
and
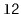
contains
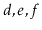
, then after calling

,
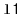
will contain
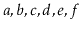
and
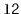
will be empty.
Exercise 3..11
Write a method
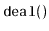
that removes all the elements with odd-numbered
indices from a
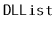
and return a
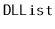
containing these elements.
For example, if
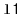
, contains the elements
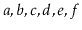
, then after
calling
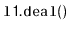
,
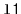
should contain
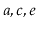
and a list containing
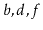
should be returned.
Exercise 3..12
Write a method,
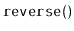
, that reverses the order of elements in
a
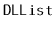
.
Exercise 3..13
This exercise walks you through an implementation of the merge-sort
algorithm for sorting a
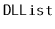
, as discussed in Section
11.1.1.
- Write a
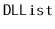 method called
method called
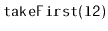 .
This method takes the first node from
.
This method takes the first node from
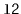 and appends it to the the
receiving list. This is equivalent to
and appends it to the the
receiving list. This is equivalent to
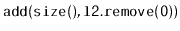 ,
except that it should not create a new node.
,
except that it should not create a new node.
- Write a
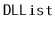 static method,
static method,
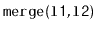 , that takes two
sorted lists
, that takes two
sorted lists
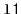 and
and
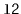 , merges them, and returns a new sorted
list containing the result. This causes
, merges them, and returns a new sorted
list containing the result. This causes
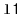 and
and
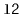 to be emptied
in the proces. For example, if
to be emptied
in the proces. For example, if
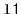 contains
contains 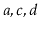 and
and
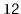 contains
contains
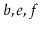 , then this method returns a new list containing
, then this method returns a new list containing
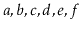 .
.
- Write a
 method
method
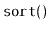 that sorts the elements
contained in the list using the merge sort algorithm.
This recursive algorithm works in the following way:
that sorts the elements
contained in the list using the merge sort algorithm.
This recursive algorithm works in the following way:
- If the list contains 0 or 1 elements then there is
nothing to do. Otherwise,
- Using the
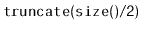 method, split the list
into two lists of approximately equal length,
method, split the list
into two lists of approximately equal length,
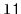 and
and
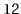 ;
;
- Recursively sort
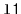 ;
;
- Recursively sort
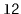 ; and, finally,
; and, finally,
- Merge
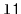 and
and
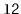 into a single sorted list.
into a single sorted list.
The next few exercises are more advanced and require a clear
understanding of what happens to the minimum value stored in a
 or
or
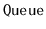 as items are added and removed.
as items are added and removed.
Exercise 3..14
Design and implement a

data structure that can store
comparable elements and supports the stack operations
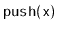
,
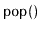
, and

, as well as the
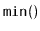
operation, which
returns the minimum value currently stored in the data structure.
All operations should run in constant time.
Exercise 3..15
Design and implement a
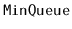
data structure that can store
comparable elements and supports the queue operations
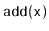
,

, and

, as well as the
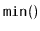
operation, which
returns the minimum value currently stored in the data structure.
All operations should run in constant amortized time.
Exercise 3..16
Design and implement a
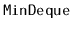
data structure that can store
comparable elements and supports all the deque operations
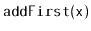
,

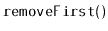
,

and

, and the
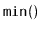
operation, which returns the minimum value currently stored in
the data structure. All operations should run in constant amortized
time.
The next exercises are designed to test the reader's understanding of
the implementation and analysis of the space-efficient
 :
:
Exercise 3..17
Prove that, if an

is used like a
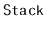
(so that the
only modifications to the

are done using
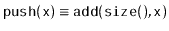
and
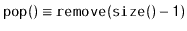
), then these
operations run in constant amortized time, independent of the value
of
.
Exercise 3..18
Design and implement of a version of an

that supports all
the
operations in constant amortized time per operation,
independent of the value of
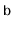
.
Exercise 3..19
Explain how to use the bitwise exclusive-or operator,
^, to
swap the values of two
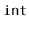
variables without using a third variable.
opendatastructures.org
![]() data structure seems to be a well-known data structures exercise.
The
data structure seems to be a well-known data structures exercise.
The
![]() is sometimes referred to as an unrolled linked list
[67].
is sometimes referred to as an unrolled linked list
[67].
![]() , contains only one
pointer, called
, contains only one
pointer, called
![]() , that holds the bitwise exclusive-or of
, that holds the bitwise exclusive-or of
![]() and
and
![]() . The list itself needs to store two pointers, one to the
. The list itself needs to store two pointers, one to the
![]() node and one to
node and one to
![]() (the first node, or
(the first node, or
![]() if the list is
empty). This technique uses the fact that, if we have pointers to
if the list is
empty). This technique uses the fact that, if we have pointers to
![]() and
and
![]() , then we can extract
, then we can extract
![]() using the formula
using the formula
![]() s.
You should complete them without allocating any new nodes or temporary
arrays. They can all be done only by changing the
s.
You should complete them without allocating any new nodes or temporary
arrays. They can all be done only by changing the
![]() and
and
![]() values of existing nodes.
values of existing nodes.
![]() or
or
![]() as items are added and removed.
as items are added and removed.
![]() :
: